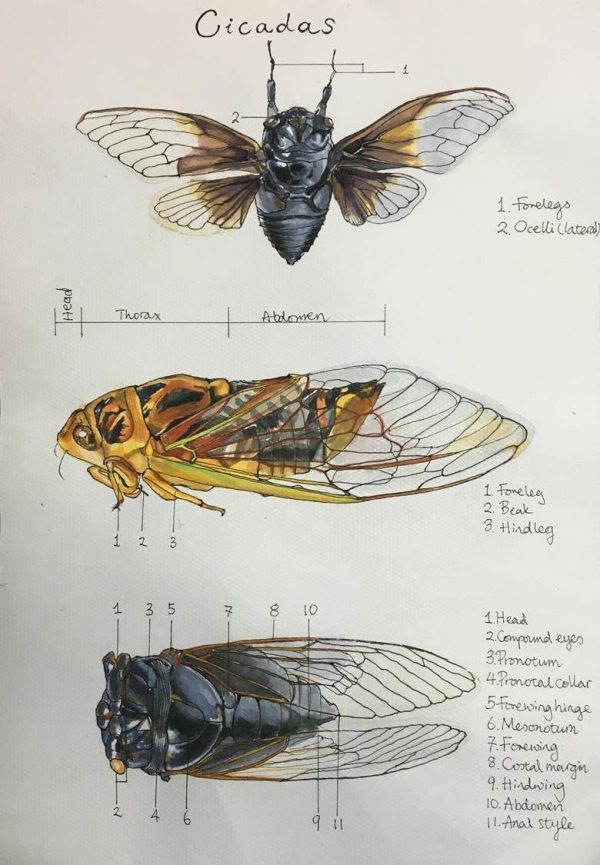
Der Gesang der Katastrophe
Anmerkungen zu Primzahlen, Zikaden und Sprachen an einem langen, schläfrigen Sommernachmittag – von Georg Seeßlen
I
Wenn man lange genug an einem späten Sommernachmittag unter diesem oder jenem Baum sitzt und nachdenkt (wie es ein nicht zu Ende befreiter Sklave gerne tut), gehen Gedanken, jedenfalls einige von ihnen, dorthin, wo noch keiner von ihnen war und wohin sie niemand geschickt hat. Es ist etwas, das einen durchströmt, als hätte man gerade alle Zeit der Welt; und die wiederum sei gerade dabei in sonderbare Einzelteile zu zerfallen. Zahlen und Reihen durchziehen das Wuchernde und Zirpende, Blätter bilden Muster und Systeme, Tiere gehen ihrer Wege, als wüssten sie genau wohin. Die jagenden streifen, die gejagten suchen Deckung, die bauenden bilden Straßen, andere kehren nach Hause zurück. Etwas lockt, anderes droht, und wieder etwas scheint einen bedeutenden Fund zu markieren. Da ist eine Ordnung im Chaos, oder das Chaos ist in der Ordnung. Und da ist das wohlige Gefühl, gerade im Augenblick nicht weiter zu stören. Jedenfalls tut diese kleine Welt am späten Sommernachmittag so, als wäre es ihr gleichgültig, ob sie gesehen wird oder nicht.

II
Der spanische Mathematiker und Schriftsteller Guillermo Martínez hat in seinem Roman „Die Pythagoras-Morde“ eine amüsant-mörderische Konfrontation zwischen zwei wissenschaftlichen Weltbildern entwickelt. (Richtig amüsant-mörderischer konnte es nur werden, weil sich die Geschichte zwischen einem alten Professor und einem jungen begabten Studenten, nebst allerlei Konkurrenten und Liebschaften, in den Campus-Mauern von Oxford abspielt, wo auch Martínez einige Jahre verbrachte und welchselbigen Schauplatz auch die Verfilmung von Álex de la Iglesias „Oxford Murders“ zu nutzen wusste.) Die eine Position geht davon aus, dass alles Mathematische nur in diesem selbstgeschaffenen System, der Mathematik eben, Geltung hat, und das, was man „Natur“ und „Leben“ nennt, sich einen Pfiff darum kehrt und als Wider-Sinniges gegen alle Berechnung rebelliert; und die andere behauptet im Gegenteil, dass alles Natur und alles Leben dem Wesen und der Praxis nach mathematisch sei, ob man das nun stets gleich bemerken kann oder nicht. Nun ja, Chaos und Regel, das alte Spiel: Jeweils ein Level höher erweist sich das scheinbar Geregelte als chaotisch, und das scheinbar Chaotische als geregelt. Wahrscheinlich, so dröhnt es aus der Botanisiertrommel unserer Träume, ist einfach die Dualität falsch.

Zwischen dem Chaotischen und dem Geordneten steht das Sonderbare. Sonderbar sind zum Beispiel Primzahlen, also Zahlen, die sich nur durch eins und sich selbst teilen lassen, und sonst gar nicht: 1,2 (die trivialen Primzahlen), 3,5,7,11,13,17,19,23… die Reihe ist bemerkenswerterweise unendlich, schon weil alle Zahlen, die aus lauter Einsen bestehen wie etwa 111111111111111111 naturgemäß Primzahlen sind. Man kann darüber streiten, ob Primzahlen Teil einer Ordnung oder Einbruch des Chaos in sie sind; es kommt, wie gesagt, auf das Level an. Im richtigen Leben jedenfalls kann man sich fragen, zu was zum Teufel Primzahlen oder das Wissen um sie gut sein sollen.
Aber spielen Primzahlen etwa in der Natur eine Rolle, die, wenn überhaupt, wohl gerade mal in den Gleichungen und Reihen „niederer Mathematik“ rhythmisiert ist: Sonnentage, Lebenszyklen, Jahresringe, Paarungszeiten, Generationenfolgen, Gezeiten, Geweihenden, Winterschläfe, Vogelrouten, explosive Populationen, Eiszeiten, Endmoränen, Lachszüge…man kann das alles mit ein bisschen gutem Willen in Zahlen ausdrücken, und in Beziehungen von Zahlen. Auch dass das Weltall sich „entwickelt“, vom Urknall bis zur Unendlichkeit, und dass es immer wieder zyklisch und pulsierend zugeht, scheint für uns ebenso festzustehen, wie gewisse „Singularitäten“. Womit wir bei der Katastrophentheorie wären.

Der britische Mathematiker Ian Stewart studierte nicht in Oxford, sondern nebenan in Cambridge und konzentrierte sich seit seinem Studienabschluss auf eben die Katastrophentheorie. Die mathematische Katastrophentheorie beschäftigt sich mit unstetigen, sprunghaften Veränderungen kontinuierlicher dynamischer Systeme. Diese können, auch wenn sie unter bestimmten Voraussetzungen einen stabilen Zustand anstreben, bei Änderungen der Parameter sprunghafte, nichtstetige, diskontinuierliche Änderungen der Lösung erfahren.
Soll also niemand sagen, die Katastrophe habe in der Mathematik nichts zu suchen; im Gegenteil, sie ist ihr ständiger Begleiter, was sich im übrigen manchmal auch sehr personal auswirkt. Wie jedes Glaubenssystem kann auch das der Mathematik das eine oder andere mal zusammenbrechen, mit verheerenden Folgen. Dabei freilich scheint es uns immer noch sehr viel einfacher, uns einen verrückt gewordenen Mathematiker (wie es ihn auch in den „Pythagoras Morden“ gibt) vorzustellen als eine verrückt gewordene Mathematik. Umgekehrt findet jeder Satz, betreffe er einen Glauben oder eine Formel, seine Fundamentalisten wie etwa Erik Christopher Zeeman, der die Katastrophentheorie mehr oder weniger als Weltformel einzusetzen versuchte und damit die Wahrscheinlichkeit von Schiffsuntergängen ebenso wie die Krisenzyklen der Warenproduktion zu erklären versprach. Am Sonderbarsten aber war die Anwendung auf die Biologie, oder, anders gesagt: Auf die Natur.
Die klassische Formel zur Illustration der Katastrophentheorie lautet
V = x3+ ax
Daraus ergibt sich für die verschiedenen Werte von a eine Lösungsreihe. Bei negativen Werten von a hat die Potentialfunktion ein stabiles und ein instabiles Extremum. Nimmt der Parameter a langsam zu, kann das System dem stabilen Minimum folgen. Bei a = 0 treffen sich die stabilen und instabilen Extrema und heben sich auf; man hat den „Bifurkationspunkt“ erreicht. Für a > 0 gibt es keine stabile Lösung mehr. Ein physikalisches System würde bei a = 0 seine für negative a vorhandene Stabilität plötzlich verlieren und sein Verhalten würde vollkommen umkippen. Würde, sagen wir einmal, die Formel die Rhythmen und Pausen des „Gesangs der Zykaden“ vor meinem Fenster beschreiben, und a entspräche irgend einem Einfluss aus der Natur (oder gar die Brahms-Suite aus meinem CD-Player), dann verlöre wohl dieser Gesang, vertraut in seiner Rhythmik und in seinen unregelmäßigen Pausen, jedes stabile Format.

Interessanterweise wählen die Mathematiker für die einfachen Formen der, nun ja, Katastrophenformel analoge Begriffe, auf eine lokales Extreme folgt „die Faltung“, die „Spitze“, der „Schwalbenschwanz“, und der „Schmetterling“; danach wird es abstrakt, nämlich eliptisch, hyperbolisch und parabolisch, und ab da haben die Versuche, den Katastrophenfall in komplizierteren Systemen wiederzugeben, überhaupt keine Namen mehr. Es scheint nur festzustehen, dass auch eine Katastrophenreihe mehr oder weniger unendlich wird und dabei ziemlich schnell den Bereich des „Vorstellbaren“ verlässt.
Wir müssen gar nicht so tun, als ob wir das verstünden. Entscheidend scheint vielmehr, dass sich Mathematik und der Rest der Welt nicht allein in den niederen Rhythmen, sondern insbesondere in den Katastrophenfällen begegnen, also auch mit der Natur – in sehr verschiedenen Weisen, wie man sie bestimmen und gegen etwas anderes abgrenzen können mag, denn „Alles ist Natur“ ist keine Aussage sondern der Mythos aller Mythen: Alles ist weil es ist, was es ist und schon immer gewesen ist). Der engere Begriff der Natur – jenseits des romantischen Zwiespalts zwischen dem Gegebenen, Wachsenden und Sterbenden und dem Gemachten, Berechneten und Rekonstruierbaren, wahlweise Kultur, Zivilisation oder einfach Technik genannt – versteht sich als selbstregulierendes Meta-System, das wiederum mehrere Systeme und Subsysteme in enthropischen Verhältnissen miteinander in Beziehung setzt. Menschen greifen in diese Systeme ein (weil es ihrer Natur entspricht), zerstören einige, machen andere von solchen Eingriffen abhängig, begreifen wieder andere, um sie zu simulieren, auszunutzen oder auszuschalten. Neben den technischen Instrumenten dienen dem Menschen dazu zwei Formen von Abstraktion. Die Sprache und die Mathematik. Beide sind indes nicht einfach weitere Instrumente, sondern habe selbst etliche Attribute einer „Natur“, insofern sie wachsen (und sterben), exzessiv differenzieren und keineswegs dem Willen ihrer „Schöpfer“ oder „Maschinisten“ gehorchen. Sprache und Mathematik sind paradoxerweise weder sagbar noch berechenbar. So wie sie sich zu einer Meta-Technik entwickeln, entwickeln sie sich auch zu einer Meta-Natur. In der Sprache und in der Mathematik kann man verloren gehen wie in einem Wald oder auf hoher See. Während man also zur gleichen Zeit versucht, die Systeme zu ihrer Kontrolle zu verbessern, wird man stets hoffen, sie auf ihre Natur zurückzuführen. Also müsse doch irgendwo und irgendwann der gemeinsame Ursprung zu finden oder wenigstens zu begründen sein: Im Anfang waren Wort, Zahl und Natur eins. Oder?
III
Jemand wie Guilliermo Martinéz versucht uns deshalb, die Sache in einer Kriminalhandlung näher zu bringen (die Mordserie wird unwissentlich durch eben jenen Menschen ausgelöst, der als einziger in der Lage scheint, ihr Muster zu erkennen; die Erklärung für den Katastrophenfall liegt im Erklärenden selber); Ian Stewart dagegen will die Natur dabei beobachten, wie sie den Katastrophenfall herbeiführt, oder wenigstens, eine Vorstudie gewissermaßen, mit den Sonderbarkeiten arbeitet. Zum Beispiel mit den Primzahlen.

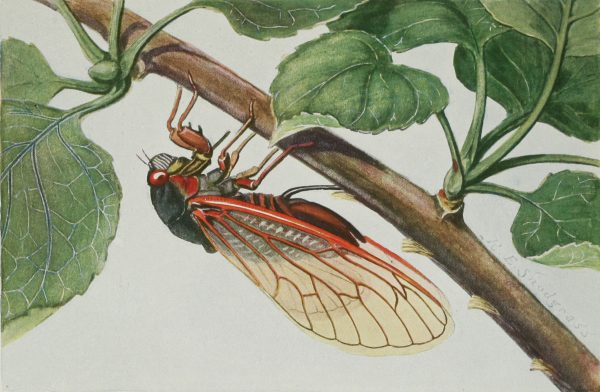
Zikaden zum Beispiel vermehren sich in diesem sonderbaren Rhythmus. Alle 13 oder alle 17 Jahre kommen die Larven aus der Erde und entwickeln sich für einen kurzen Sommer zu den erwachsenen Tieren, die wir kennen. Dass sie gerade im Rhythmus von Primzahlen diese Transformation vornehmen, scheint ein besonders genialer Trick, sich vor den Fressfeinden zu schützen, die auf das Überangebot reagieren. Denn eben diese Fressfeinde vermehren sich in Rhythmen von zwei, vier, fünf oder sechs Jahren, so dass es zu keiner häufigen Synchronität kommt. Schlüpft ein Fressfeind zum Beispiel im Fünf-Jahresrhythmus, dann dauert es mindestens 85 Jahre, nämlich 5 mal 17 Jahre, bis sich die Schlüpfzyklen von Zikaden und Fressfeinden überschneiden. Andere Zikaden-Arten haben einen 7-Jahresrhythmus. Entstanden sind diese Zyklen offenbar durch einen genetischen Zufall; die Primzahl erwies sich dabei sozusagen als positiver Katastrophenfall, der eine hohe Überlebensrate für eben jene Mutation brachte. Nun freilich kommt die Pointe: Eben jene Fressfeinde, denen die Zikaden mit ihrem Primzahlen-Rhythmus ein Schnippchen schlagen, sind schwer oder gar nicht auszumachen. Damit die Theorie also wieder stimmt, muss man davon ausgehen, dass zumindest die gefährlichsten dieser Fressfeinde gar nicht mehr existieren. Man geht derzeit von einer ausgestorbenen Wespenart aus. Und ausgestorben kann diese Wespenart offensichtlich nur deswegen sein, weil ihr das bevorzugte Beutetier, die Zikade, durch ihren Vermehrungsrhythmus die Nahrungsgrundlage raubte. So also könnten, wenn die Theorie stimmt, die Schwachen durch Mathematik die Starken vernichten. Aber am Anfang war das alles nichts als ein dummer Zufall, und am Ende ist es eine mehr oder weniger sinnlose Verhaltensweise, die vielleicht bloß auf einen neuen Katastrophenfall wartet.
Vielleicht steckt aber noch ein drittes in diesem Primzahlen-Zyklus: Ein Lebenszyklus, der auf einer Primzahl basiert, findet sozusagen für seine Protagonisten immer wieder neue, unvorhergesehene Lebensumstände vor, jedenfalls für den kurzen Abschnitte der Vermehrung vor dem Tod. Ob das der Zikade nutzt oder bloß neue Risiken birgt, ist eine sehr menschliche Frage. Das Verhältnis der Zikade zu ihrer Umwelt jedenfalls bleibt auf diese Weise sonderbar. Es ist dafür gesorgt, dass nicht einfach immer wieder nur das gleiche passiert.

IV
Je nun, mag man denken an einem späten Sommernachmittag unter diesen oder jenen Bäumen und beim Gesang der Zikaden, die sich wahlweise gegenseitig bedrohen und anlocken, auch hier haben wir es mit zwei Extremen zu tun, die alternierend auftreten: Erscheinungen der Stabilität und solche der Instabilität. Ab einer bestimmten Anzahl von Parametern und in bestimmten Formen ihrer Abhängigkeit voneinander, eingedenk des Wirkens der Primzahlen als „Naturzahlen“, deren Verhalten im Wesentlichen immer noch nicht vollständig geklärt ist, scheint eine Unterscheidung zwischen Zufall und Notwendigkeit nicht mehr zweifelsfrei zu treffen, auch nicht in der uns gemäßen Art, nach der sich das Mega-System Natur immer die nützlichen Zufälle zueigen macht, die unnützen (für die Stabilität des ganzen) indes einfach wieder vergisst. Die kollektive Ermordung des Fressfeindes durch den Primzahlen-Lebenszyklus mochte für die Zikaden überlebensnotwendig sein, doch die Folgen sind chaotisch. Es wäre schließlich auch zu überlegen, welche Lücke die ausgestorbene Wespe im System hinterlässt – vom Sieg der Zikaden abgesehen; die wiederum durch ihre Primzahlen-Zyklen in ihrer Vermehrung gebremst werden.
Die emotionalen Extreme des Menschen in der Natur sind: Sich in ihr zuhause fühlen, Sich in ihr fremd fühlen. Manchmal empfindet man beides zugleich, oder genauer gesagt: das eine ist eine Funktion des anderen, wie in einer Formel der Katastrophentheorie. Beständig fragt man sich daher, ob die Natur als Lebensmetapher taugt oder nicht. Ist der Kapitalismus, zum Beispiel, wirklich eine zweite Natur? Ist es „Natur“, was der künstlichen Intelligenz fehlen wird (Tod, Schmerz, Vernichtung, Katastrophe), und kann man mithilfe der Primzahlen wiederum „Natur“ (Zufall, organische Wucherung, Mimikri etc.) erzeugen, ist mithin die Primzahl ein geheimes Band zwischen Natur und Kultur, Materie und Abstraktion?

Etwas ähnliches wurde ja schon einmal mit der Fibonacci-Reihe versucht, in der jede Zahl die Summe der beiden vorherigen ist. (1, 1, 2, 3, 5, 8, 13, 21, 34 …) Am Blütenstand verschiedener Blumen, darunter das verbreitete „Gänseblümchen“, wiederholen sich gegenläufige Spiralen nach Fibonacci-Verhältnissen (in diesem Fall eine Reihe mit 21 und die nächste mit 34 Elementen), ähnliches lässt sich für Kiefernzapfen oder Ananansfrüchte feststellen. Leider gibt es dafür keine so schöne Geschichte wie bei den Zikaden, stattdessen aber eine Beziehung zur Ästhetik: Fibbonacci-Zahlen verhalten sich zueinander im Verhältnis von 1 zu 1,6, was ziemlich genau dem Verhältnis des Goldenen Schnitts entspricht, mit dem wir uns eine der Grundlagen von „Schönheit“ erklären.

Als Parameter der Natur ist die (Menschen-) Kultur der Katastrophenfall, als Parameter der Kultur ist die Natur der Katastrophenfall, was die Begegnung miteinander anbelangt. Wo sich Kultur und Natur begegnen, kommt es zu der sprunghaften und unberechenbaren Reaktion, von der die Katastrophentheorie spricht. Katastrophe meint ja hier nicht allein das Zerstörerische, sondern vor allem das Anti-Systematische, eben das, was nicht Wiederholung und stabile Entwicklung ist. Jedes Denken über sie, mag man unter diesem oder jenem Baum an einem späten Sommernachmittag zum Gesang der Zikaden denken, erzeugt und vernichtet Natur, man entfernt sich, wenn man auf sie zugreift, und man nähert sich ihr durch Distanz. Außer natürlich, man liegt nur so da, mittendrin, und hofft, nicht weiter zu stören – was sich indes beim ersten Mückenstich als Illusion erweist.
Nun ist auch diese Metapher zu überprüfen. Denn beide System haben ihren Katastrophenfall keineswegs nur im jeweils anderen, sondern entwickeln ihre Reihen jeweils auf Katastrophenfälle hin. In beiden Fällen nämlich handelt es sich um wachsende Systeme, enthropische Vereinnahmungen inklusive. Wenn wir sie nur ließen, würde die Natur sich weiter differenzieren und womöglich nicht nur lustige und sonderbare Dinge wie Faultiere oder eben Zikaden hervorbringen, sondern womöglich ein Monstrum, dass für seine Umwelt genau so gefährlich wäre wie der Mensch. Wenn die Erde ein geschlossenes System bildet (was sie streng genommen aber nicht ist), dann wäre der Selbstregulierung der Natur eben das Prinzip der Katastrophenfälle entgegengesetzt, nach denen nichts mehr so ist wie vorher. Der Verdacht liegt also nur allzu nahe: Der Mensch ist der Katastrophenfall der irdischen Natur, aber eben nur einer von vielen Möglichkeiten. Die Fähigkeit zum Überlisten und zum Codieren mag sich dabei verhalten wie der Primzahlen-Zyklus der Zikaden in der ersten Theorie: Der Erfolg macht die Sache selbst sinnlos. Und von ihm aus gesehen verhält es sich so, dass die Natur der Katastrophenfall für sein eigentliches Wesen ist, nämlich sich von der Natur vollkommen zu lösen (Maschine, Idee, Programm, Gott und was weiß ich zu werden). Daran, dass sie zugleich Leben generieren und der Wissenschaft gehorchen soll, scheitern die Codes der Natur. Ob ihnen das egal ist wie es einer Zikade egal ist, ob man hinter das Geheimnis ihrer Primzahlen-Zyklen gekommen ist oder sich das ganze nur zurechtgelegt hat?

Primzahlen „bergen“ nicht nur Geheimnisse, sie sind auch die bislang gebräuchlichsten Übermittler von Geheimnissen, von den Geheimcodes beim Militär bis zur Datenübermittlung im Internet. Sind die Primzahlen im Lebenszyklus der Zikaden also ein Instrument, sich für die Umwelt „unlesbar“ zu machen, zugleich aber auch ein Instrument, durch Hybridisierung auf die Geheimnisse der Umwelt zu reagieren? Ein Vorgang der Codierung: Verschlüsselung und Entschlüsselung. Wir erinnern uns an den Fall der geheimnisvollen „Primzahlen-Zwillinge“, von denen Oliver Sacks berichtete: Für das richtige Leben schienen sie nicht geschaffen, aber in ihrer Kommunikation spielte lustvoll die Kenntnis von Primzahlen und ihrer Umgebung die zentrale Rolle. Sie lebten in einer Welt der Primzahlen und freuten sich über jede neue Entdeckung wie über ein Tier oder eine Pflanze in einer imaginären Natur. Für ihre Umwelt blieb diese Gabe nicht nur intellektuell ein Rätsel (John und Michael stellten jeden Mathematiker und jedes Computerprogramm in den Schatten), sondern auch emotional, denn offensichtlich fanden die beiden in ihren Zahlen vor allem Schönheit.
Durch die Primzahlen-Zyklen bleiben die Zikaden den Feinden ein Rätsel. Das würde belegen, dass Natur am Ende aus Sprache besteht. Und das wiederum hieße, dass sie etwas zu sagen hätte, was nicht sie selbst wäre. Die Alten nannten dies die Götter. Uns dagegen ist heimelig und zugleich fremd das Bild, das nur sich selbst meint. Natur ist ein Bild, das nichts bedeutet. Aber etwas, das nichts bedeutet, ist ebenso unerträglich wie das Chaos, das Primzahlen in der Sprache der Mathematik anrichten. Darum vielleicht erfüllen uns Entschlüsselungen wie die Primzahlen-Zyklen der Zikaden mit solch freudiger Beruhigung, und darum gewinnt man aus solchen Beobachtungen immer so rasch eine Metapher für den Überlebenswillen. Nun scheint immerhin sinnvoll, was die nächste Metapher hergibt: Dass Zufall und Chaos nutzbringend in semantische und soziale Systeme eingebaut werden können. Vorausgesetzt, man ist nicht gerade in Oxford in eine Reihe von Morden verwickelt.
Nachdem allerlei Getier sich an seinem Körper zu schaffen machten, floh der Mensch, der unter diesem oder jenem Baum an einem späten Sommernachmittag nicht zu stören gehofft hatte. Der Sinn der Natur, dachte er, ist, in ihr nicht verloren zu gehen.
Georg Seeßlen
Georg Seeßlen: Jahrgang 1948 und in München Kunstgeschichte und Semiologie studiert, ist einer der letzten Enzyklopädisten unserer Tage. Die Bandbreite seiner sensibilité universelle, wie das bei Diderot geheißen hätte, spiegelt sich in seinen Arbeiten, sei es zum pornografischen oder zum Cop-Film, überhaupt alles mit Film, von Spielberg, Tarantino, Kubrick oder David Lynch bis Schlingensief, überhaupt Schlingensief, dazu Kritisch-Erhellendes über Untote, Volksmusik, Populär- und Hochkultur, Kriegsbilder, televisionäre Dummheiten oder Rechtsextremismus, Blödmaschinen und Geld frisst Kunst – Kunst frisst Geld, die Prostitution Bayerns durch den Fremdenverkehr und alles Sonstige aus unserem Wahnsinn, überhaupt dem Wahnsinn. Ein Schädel, der in keine Schublade passt. Seeßlen wohnt im Allgäu – und ist trotzdem weithin präsent. Seine WIKIPEDIA-Seite, seine Texte bei CulturMag
Besonderer Hinweis aus dem CulturMag Special „Verlust UNO“ auf seine Theorie: Verlust des Verlustes. Eine hauntologische Grille.